mathematical intuition for transformers

Transformers have been the major architecture driving huge advances in the field of deep learning and have also been found to effectively scale to billions of parameters. In this post, I try to mathematically break the down the core concepts of the transformers architecture like self-attention, residual stream and flow of inputs through the layers.

high-level overview

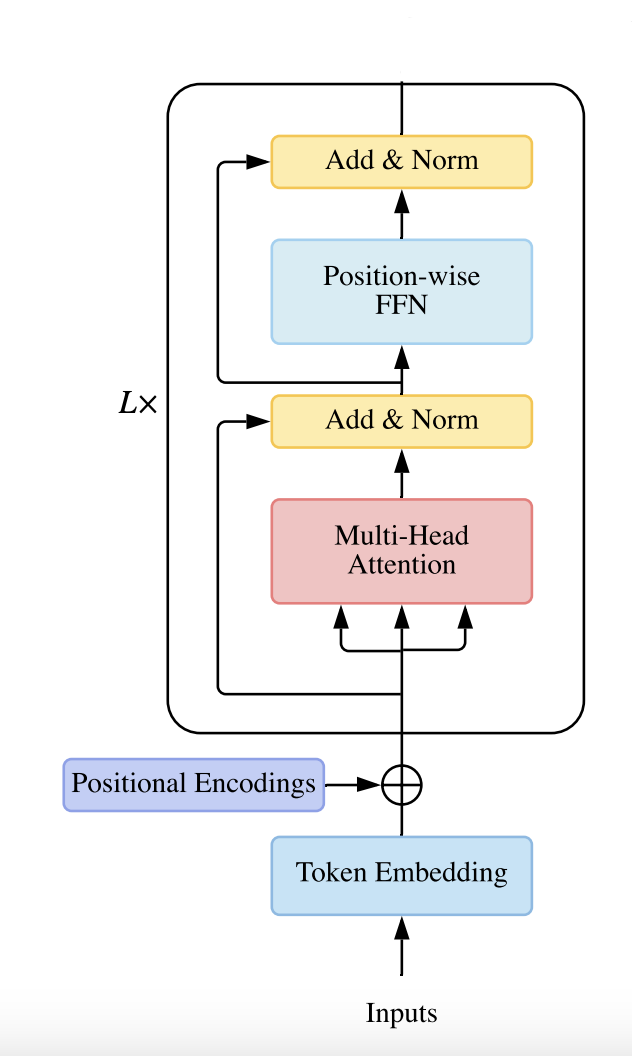
• A transformer starts with a token embedding (representing a token by a $k$ dimensional vector), followed by a series of "residual" blocks and finally a token unembedding. Each residual block consists of an attention layer followed by an MLP layer. Both the attention and MLP layers "read" their input from the residual stream and then "write" their result to the residual stream by adding a linear projection back in. Each attention layer consists of multiple heads which operate in parallel.

• The self attention along with MLP layer is called a "residual block". The residual stream refers to the flow of token representations as they pass through the layers of the transformer. Instead of re-writing the input completely with new information/representation, each layer just reads from the stream, processes it and then writes additively back into the stream which allows for information to be preserved across layers.

• The input to any residual block is token embedding or the output of the previous residual block. Each layer in the residual block takes the current token embedding from the residual stream as input. After processing the token embeddings, the output of each layer (attention or MLP) is "written back" to the residual stream. The attention layer processes the token embeddings and the output of its layer to the residual stream and then that output becomes input to the next (MLP) layer. The MLP layer also reads the new input from the previous layer from the residual stream, processes it and adds/"write" it back to the stream. This doesn't completely replace the original input but is done additively to maintain original token representation while also incorporating new information learned by the attention or MLP layer. The processed output is added to the original input. Information is always feedforward.

• A LayerNorm is applied to the input before the attention or MLP layer to stabilize training by normalizing the inputs activations (a mean of 0 and a variance of 1)

• Mathematically, for a residual block with LayerNorm before attention & MLP layers with input x,
  • Normalizing the input activations,

  $$x'= LayerNorm(x)$$

  • The output from the attention layer is added/"written" back to the residual stream,

  $$y = x' + Attention(x')$$

  • LayerNorm is applied to the above output before it goes into the MLP,

  $$y' = LayerNorm(y)$$

  • The MLP processes the normalized input $y'$ and the output is again added back to the residual stream which is the output of a residual block,

    $$y''= y' + MLP(y')$$

• Note that a Linear projection transforms the input by multiplying it with a weight matrix. It maps input from one space to another, changing the dimensionality or transforming its representation. $Linear\: projection(X),\:y = WX + b$
  where :
  $X$ is the input (or token embedding), $W$ is the learnable weight matrix and $b$ the optional bias term.

• The $MLP$ layer is a fully connected feed-forward network which consists of two linear transformations with a $ReLU$ activation in between.

• Both the attention and MLP layers each “read” their input from the residual stream by performing a linear projection means that the the input token embeddings are linearly transformed before being used for the attention mechanism or MLP's feed-forward processing.

• The token embedding X is projected into queries, keys and values matrices using linear projection, $Q=XW_Q\:\:\:K=XW_K\:\:\:V = XW_V$

• The attention mechanism then computes the attention scores and applies them to values V,

• The output of attention mechanism can be thought of as a weighted sum of the values.

• a residual block of a transformer,

self-attention

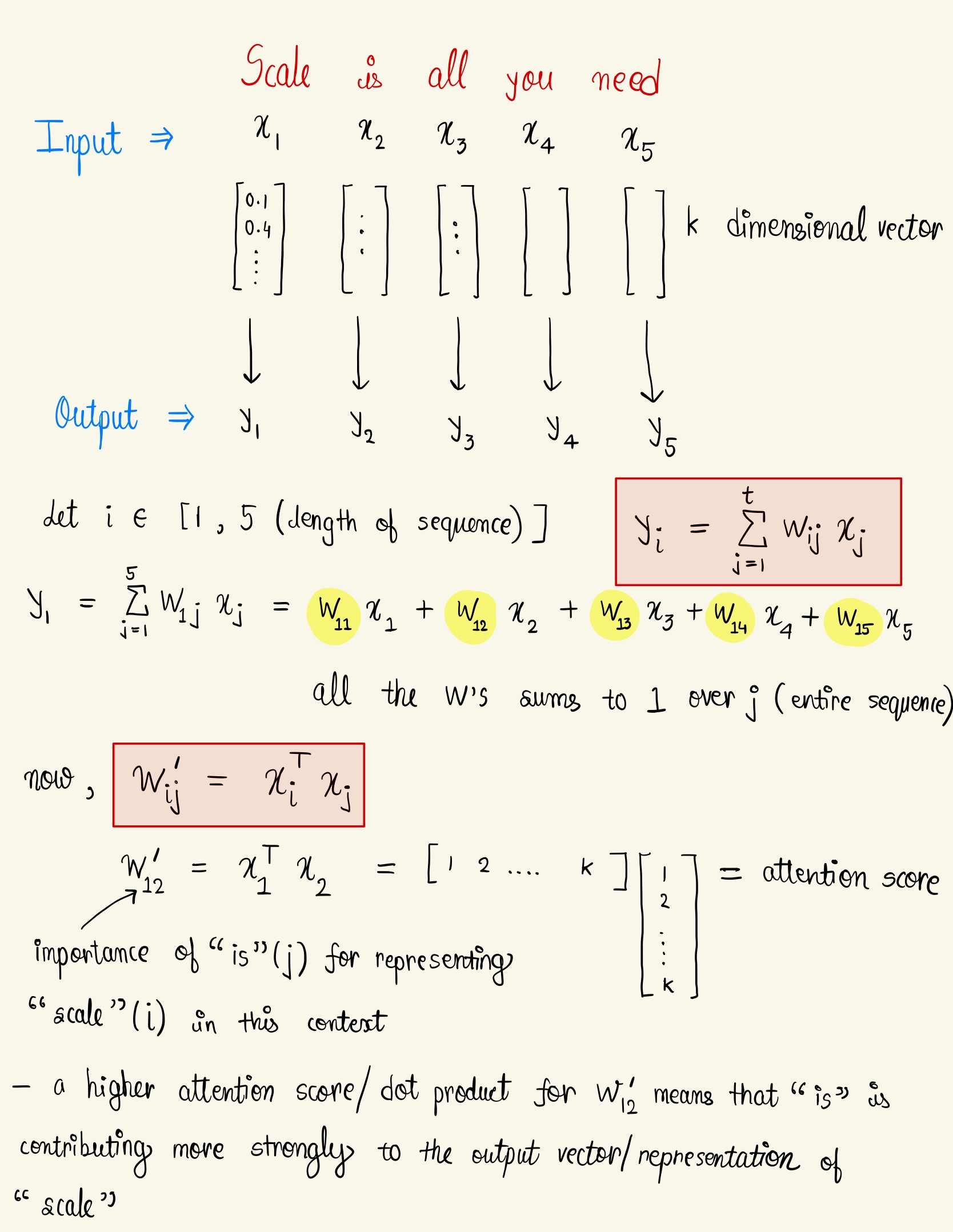
• self-attention is a sequence to sequence operation : a sequence of vector goes in and a sequence of vector comes out. Let's call the input vectors $x_1, x_2,... x_t$ and the output vectors $y_1, y_2,... y_t$ The vectors all have dimension $k$.

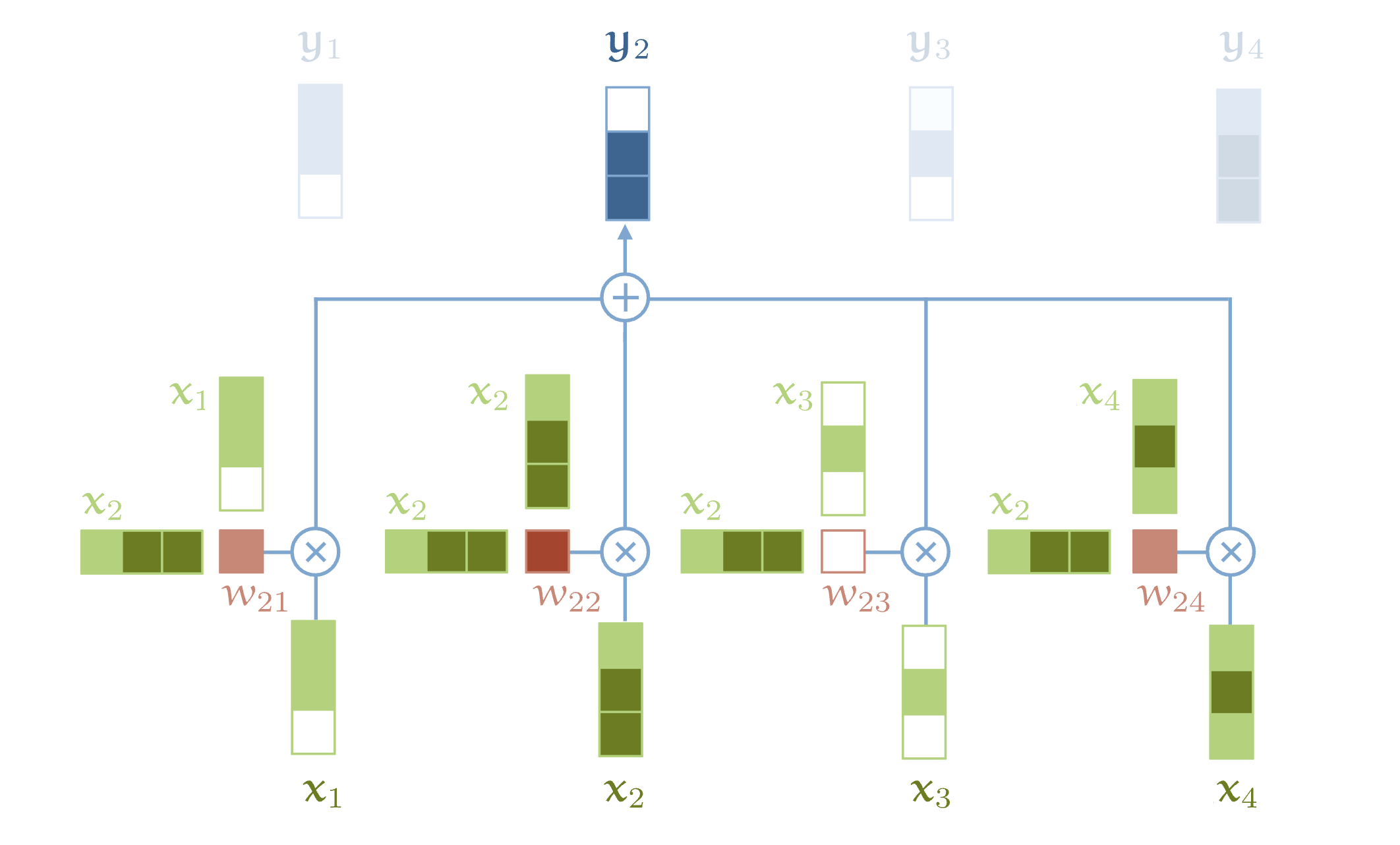
• To produce output vector $y_i$, the self attention operation takes a weighted average over all the input vectors $y_i = \sum_j w_{ij}x_j$
  where
  $j$ indexes over all the whole sequence and the weights sum to one over all $j$.

• The weight $w_{ij}$ is not a fixed parameter, but is derived from a function over $x_i$ and $x_j$ which is a dot product. It represents the strength of relationship between position $i$ and $j$ in the sequence and represents the raw "attention-scores". $w_{ij}' = x_i^Tx_j$
  
  $x_i$ is the input vector at the same position as the current output vector $y_i$. For the next output vector, you get an entirely new series of dot products, and a different weighted sum.

• the output vector $y_i$ is a new representation of $x_i$ that takes into account its relationship with all the other words in the input sentence.

• the dot product $x_i^Tx_j$ expresses how related two vectors in the input sequence are. It can also be thought of as a measure of similarity or "alignment" between the two vectors $x_i$ and $x_j$. A higher dot product means that the vectors are more aligned meaning high relevance.

• A softmax function is applied to the dot product $w_{ij}'$ to map the values between $[0,1]$ and to ensure that they sum to 1 over the whole sequence.

• Note that the values in the embedding weight matrix $W_E$ are learned during training and the dimension of the embedding weight matrix $W_E$ is $[vocab\:size, d_{model}]$, where each row represents the embedding vector $x_t$ for a token $t$ in the vocabulary. How "related" two tokens are is entirely determined by the task that you're learning/ training for.

• Self-attention treats its inputs as a set of elements rather than an ordered sequence meaning it doesn't inherently consider the order in which elements appear. It is permutation equivariant meaning that if you shuffle the inputs elements, the output elements will also be shuffles in the exact order.

• Every input vector $x_i$ is used in three different ways in the self-attention operation :
  • it is compared to every other vector to calculate the weights for its own output $y_i$. $(Query)$
  • it is compared to every other vector to calculate the weights for the output of the $j^{th}$ vector $y_j$. $(Key)$
  • it is used as a part of the weighted sum to compute each output vector once the weights have been calculated. $(Value)$

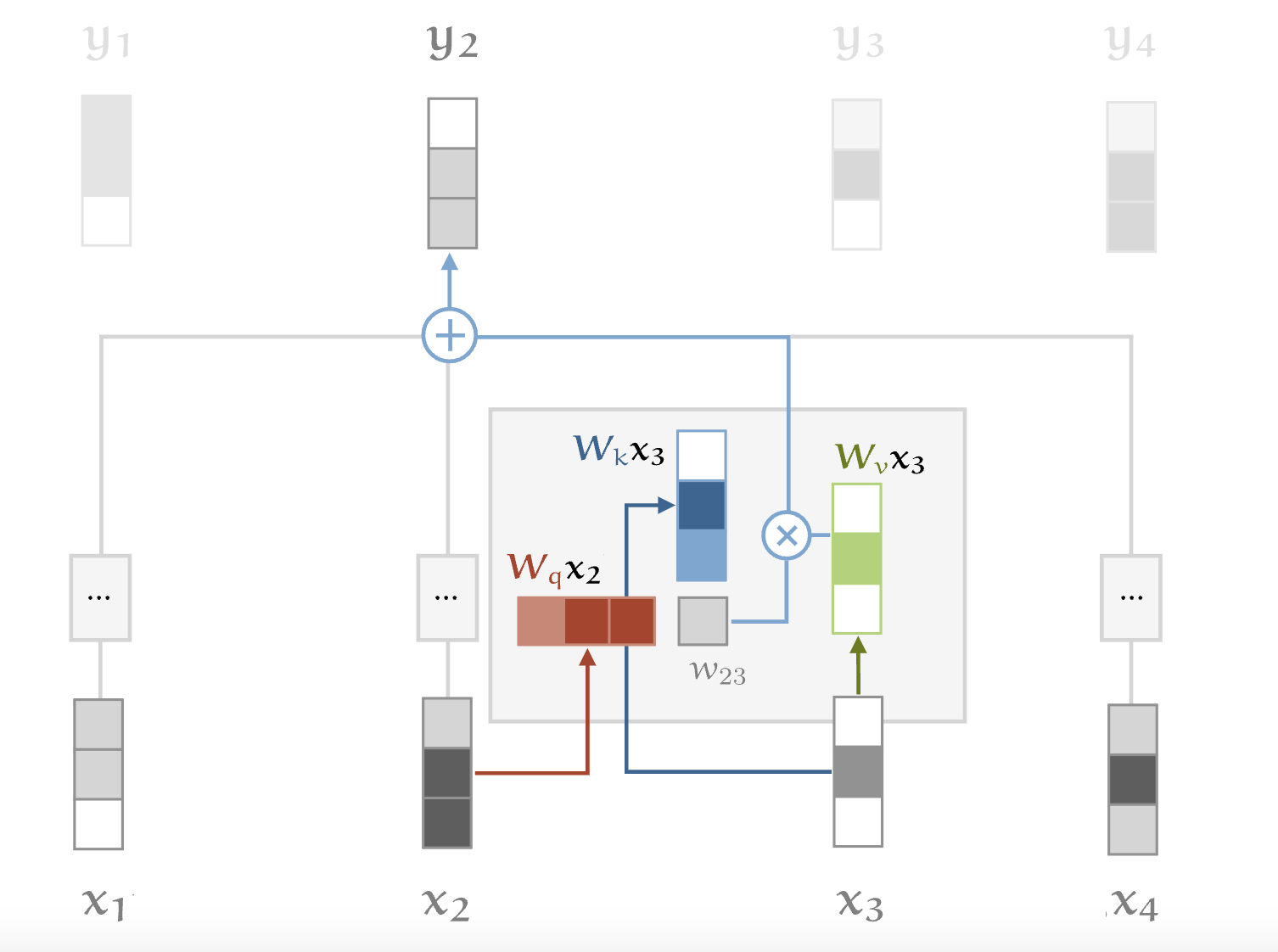
• we compute three linear transformations for the original input vector $x_i$ by multiplying it with three $(k×k)$ learned matrices $W_Q, W_K, W_V$ that transform the input into specialized representations for three different roles in self-attention :

• The query vector, $q_i$ represents what the input vector $x_i$ is looking for in other input vectors and is used to to compute attention scores with all other input vectors. It basically consists information about what to look for in other input tokens.

• The key vector, $k_j$ represents how $x_j$ presents itself to other input vectors that is the relevance or importance of $x_j$ to other vectors. It tells you what does it itself represent and how it'll contribute to other input token's representation.

• The value vector, $v_j$ is used to compute the output vector as a part of the weighted sum. It is basically a representation of $x_j$ that is actually used to compute the output vector of $x_i$ in the weighted sum.

• the dot-product $q_i^Tk_j$ helps the tokens to "attend" to other tokens that is how relevant is each token to every other token. The output is calculated by a weighted sum of the attention scores with the value vector.

• In practice, we compute the attention function on a set of queries simultaneously, packed together into a matrix $Q$. The keys and values are also packed together into matrices $K$ and $V$.

Scaled dot-product

• The softmax function is very sensitive to large input values as the exponential growth is very rapid for positive values and almost zero for negative values which kills the gradient and slows down training. If the dimension of the embedding vector is $k$, then imagine a vector in $\mathbb{R}^k$ with values all $c$. Its euclidean length is $c\sqrt{k}$. So it helps to scale the dot product back by the amount by which the increase in dimension increases the length of average vectors and stop the inputs to softmax from growing too large.

Multi-head attention

• In a single self-attention operation, all the contextual information gets combined together.

• By applying several self-attention mechanisms in parallel, each with their own key, query and value matrices $W_i^Q \in \mathbb{R}^{d_\text{model} \times d_k}, W_i^K \in \mathbb{R}^{d_\text{model} \times d_k}, W_i^V \in \mathbb{R}^{d_\text{model}\times d_v}$ we can capture diverse relationships between the input tokens and their influence in different ways. These are called attention heads.

• In multi-head attention, each head receives low-dimensional keys, queries and values. If the input vector has $d_{model}=256$ dimensions and we have $h=4$ attention heads, then $d_k = d_v = d_{model}/h = 64$ to project them down to a 64 dimensional vector (since the input vectors which is 256 dimensional vectors are multiplied by a $256\times{64}$ weight matrices). While projection cannot perfectly preserve all the information from the higher dimensional space, the 4 different heads focus on different aspects of the input.

• Multi-head attention allows the model to jointly attend to information (i,e, focus on different aspects of the input simultaneously) from different representation subspaces (since each head is projected to a different lower dimensional space) at different positions (different parts of the input sentence).

• The outputs from all attention heads are then concatenated combining all the information from different subspaces that each head has focused on (bringing the lower dimensional back up to $d_{model}$). Then the combined output is projected using the weight matrix, $W_O$ where $W_i^O \in \mathbb{R}^{hd_v \times d_\text{model}}$ which serves to transform the concatenated output into the appropriate dimensionality for the next layer and since its a learnable matrix it allows the model to learn how to best combine the information from different heads and capture more complex relationships between the features extracted by different heads.

Positional Encoding

• Since self-attention is permutation invariant, positional encodings help encode information about the relative or absolute position of the tokens in the sequence. The positional encodings have the same dimension $d_{model}$ as the embeddings, so that the two can be summed. They're not learned unlike word embeddings but generated by a predefined function.

• The function f : $pos \in ℕ → ℝ^k$ maps position to $k$ dimensional vector. A sine or cosine function of different frequencies can be used :

• where $pos$ is the position in the sequence and ${2i}$ and $2i +1$ represents even and odd dimensions (indices) in the vector.

• The sinusoidal function allows the model to extrapolate to sequence lengths longer than the ones encountered during training. For any fixed offset $k$, $PE_{pos+k}$ can be represented as a linear function of $PE_{pos}$. This property helps the model to easily learn to attend by relative position rather than absolute position and helps the attention learn a general pattern of "attend to k steps away" rather than learn for each absolute position pair.

References

• Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., Kaiser, L., & Polosukhin, I. (2017, June 12). Attention is all you need. arXiv.org. https://arxiv.org/abs/1706.03762

• Transformers from scratch | peterbloem.nl. (n.d.). https://peterbloem.nl/blog/transformers